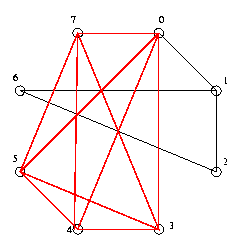
Supposons que l'environnement soit représenté par le schéma suivant :

On dispose donc d'une carte en mémoire qui donne la position des 21
portes .

Supposons maintenant que le robot soit représenté par le disque R, orienté selon la flèche. Les portes en rouge sont celles qui sont visibles de cette position du robot.

Une fois la position des portes détectée (par rapport au robot), on obtient une carte locale, comme ceci :

Le problème est alors d'identifier les portes visibles sur la carte locale.
L'utilisation d'un graphe de correspondance permet de trouver une solution fiable au problème de l'identification. Dans un tel graphe, les noeuds sont les mises en correspondance potentielles (un noeud représente l'appariement Porte 1 -- Porte IV). Ensuite, on ajoute des arcs entre les noeuds de ce graphe lorsque les noeuds sont cohérents entre eux. Par exemple, la position relative de la porte 14 par rapport à la 6 est la même que celle de la porte I par rapport à la IV, les appariements (14,I) et (6,IV) sont donc cohérents, on ajoute donc un arc entre les noeuds qui les représentent.
Une fois les arcs construits, on recherche un sous ensemble de noeuds de taille maximale, tel que les noeuds soient tous cohérents entre eux. Ce sous ensemble correspond à un sous graphe complet (tous les noeuds connectés à tous les autres).
Problème : la recherche d'un sous-graphe complet de taille maximale (une clique maximale) est un problème NP-complet (très très difficile à résoudre) dans le cas général. Cependant, si le critère de cohérence utilisé pour construire les arcs est suffisamment discriminant, le graphe résultant est suffisamment simple pour qu'une clique soit trouvée en un temps compatible avec un traitement temps réel.
Le but de cette bibliothèque est d'implémenter une représentation des graphes et l'algorithme de recherche d'une clique maximale. L'algorithme est inspiré des indications trouvées sur le site : The Algorithm Design Manual.
Attention : L'algorithme utilisé n'est pas du tout économe en mémoire. Quand c'est possible, il vaut donc mieux faire une préselection des repères potentiellement visibles, et réduire ainsi la taille du graphe.
La recherche se fait en deux fois. On recherche d'abord une clique maximale, puis on cherche s'il existe une clique plus grande. A chaque étape, on élimine les noeuds dont le degré n'est pas suffisant. Globalement, l'algorithme est le suivant :