A Grenoble, le réseau de bus/tram est assez complet et redondant pour que je puisse aller de chez moi à la gare SNCF par 6 itinéraires différents utilisant 5 lignes de bus. Alors à chaque fois qu'on a besoin d'aller à la gare pour un horaire précis, soit on prend les 5 livrets d'horaires et on évalue chaque itinéraire, soit on prend 20 minutes de marge et on choisit au hasard...
Alors un jour, je me suis proposé de rentrer les horaires dont j'avais besoin sur l'ordinateur et d'utiliser un algorithme de "plus court chemin" pour choisir au mieux l'itinéraire. Optimiste, je croyais vraiment que ça ne serait pas compliqué...
Cependant, au lieu de créer un logiciel qui réponde uniquement à mes besoins, ma formation de génie logiciel m'a poussé à faire quelque chose de très générique : un logiciel capable de rechercher des itinéraires optimaux sur le réseau réel complet de Grenoble, et même sur un réseau de bus quelconque.
Spécificité du problème traité : mon problème est d'arriver à l'heure, voire un peu en avance. Parmi les données de l'algorithme, il y a donc une heure limite à ne pas dépasser pour l'arrivée. Il pourrait aussi être intéressant de trouver le plus court chemin, sachant qu'on est dans l'abris-bus à partir d'une heure donnée...
Il y a deux types de difficultés dans ce projet : les difficultés liées à la spécificité du réseau de bus grenoblois et celles liées à la notion de plus court chemin sur un tel réseau. Et puis, il y a aussi le fait qu'au moment où j'ai commencé ce projet, je ne connaissais rien aux bases de données, ce qui m'a amené à gérer "à la main" le stockage et la lecture des données du réseau.
Tout d'abord, au niveau physique, le réseau pose des problèmes :
Certains arrêts ne sont desservis que dans un seul sens (Aller ou Retour), ce qui impose des comportements particuliers : pour atteindre un tel arrêt, il peut être nécessaire de le dépasser dans un sens puis de reprendre la même ligne mais dans l'autre sens.
Certaines lignes utilisent la même rue, elles partagent donc une succession d'arrêts. De même, il existe des lignes qui partent d'un arrêt commun et arrivent à un arrêt commun mais sans utiliser le même parcours. Il faut donc déterminer le meilleur endroit où prendre une correspondance, de façon à minimiser le temps de trajet total, tout en maximisant le temps de correspondance.
Ensuite, au niveau de la définition des horaires :
Les fiches d'horaires des lignes classiques ne donnent pas l'horaire de passage à tous les arrêts de la ligne mais à 5 ou 6 arrêts clefs. Entre ces arrêts, il faut donc interpoler.
Autre particularité des fiches d'horaires, il existe des périodes (blanche, verte, bleue et orange) qui définissent des horaires particuliers. Ces périodes sont définies par des jours de la semaine ou des périodes de l'année et sont spécifiques à chaque ligne.
Certaines lignes n'ont pas d'horaires fixes. Ainsi, les fiches d'horaires des tramways indiquent "un tram tous les 4 à 5 minutes". L'utilisation de ces données dans le choix d'un plus court chemin n'est pas évidente.
Finalement, l'intégration de tous ces paramètres dans un algorithme de recherche du meilleur itinéraire s'est révélée complexe.
Tout d'abord, je n'ai pas voulu utiliser d'heuristique, ceci pour être sûr d'avoir le meilleur trajet. La complexité est bornée en limitant le nombre maximum de correspondances : globalement, les réseaux de bus sont "étoilés" et on peut toujours aller d'un arrêt à un autre en 3 (voire 4) correspondances.
Ensuite, la notion de plus court chemin est particulière : le réseau de bus ne définit pas un graphe dont on peut valuer les arêtes. En effet, le temps de trajet entre deux arrêts dépend des lignes choisies et des temps de correspondance. On ne peut valuer le graphe que lorsque l'itinéraire optimal est connu.
Enfin, cet algorithme doit prendre en compte les lignes avec des horaires génériques et les arrêts qui ne sont desservis que dans un seul sens.
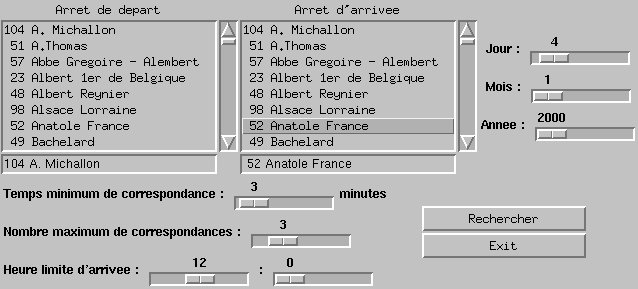
Données de l'algorithme
- Un arrêt de départ et un arrêt d'arrivée.
- Le jour du voyage, pour choisir la période.
- L'heure à laquelle on veut arriver au plus tard. Sachant qu'on veut arriver le plus tard possible en voyageant le minimum de temps.
- Le temps minimum que l'on veut avoir à chaque correspondance.
- Le nombre maximum de correspondances accepté.
Gestion des horaires
Les horaires des lignes classiques sont interpolés par rapport aux horaires de passage aux arrêts de référence. Les arrêts intermédiaires sont supposés équidistants, ce qui forme une approximation raisonnable en pratique.
Pour les horaires génériques, on fait aussi une interpolation, non sur le moment du passage, mais sur la durée du voyage entre deux arrêts. Si on ajoute ensuite la fréquence de passage à la durée interpolée, on obtient une borne supérieure au temps Attente + Voyage. Le voyage sera sûrement plus court mais l'heure limite d'arrivée ne sera pas dépassée.
Plus court chemin
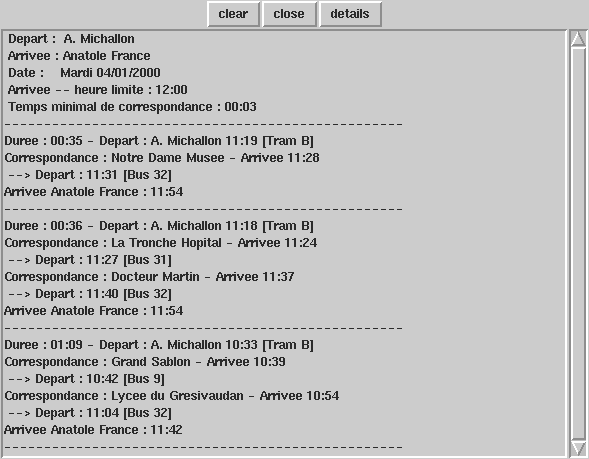
La recherche du plus court chemin se fait en deux étapes : on recherche d'abord quelles successions de lignes mènent du départ à l'arrivée, puis on cherche pour chaque succession quelle serait la durée minimale du voyage. Les itinéraires sont ensuite affichés du plus court au plus long.
Pour rechercher les successions de lignes utilisables, on part de l'arrêt de départ et on regarde quelles sont les lignes présentes. Pour chacune de ces lignes, on regarde si elle permet d'atteindre l'arrêt de destination. Si oui, on a un itinéraire valide, sinon, on regarde quelles sont les lignes qu'elle permet d'atteindre et on itère jusqu'à atteindre le nombre maximum de correspondances. Cette partie est la partie la plus coûteuse de la recherche. C'est ici qu'il serait intéressant d'ajouter une heuristique pour limiter le nombre d'itinéraires considérés.
Pour traiter un itinéraire (succession de lignes), on utilise une structure de treillis : ce treillis represente l'ensemble des chemins possibles pour aller d'un arrêt à un autre en passant par une liste fixée de ligne.
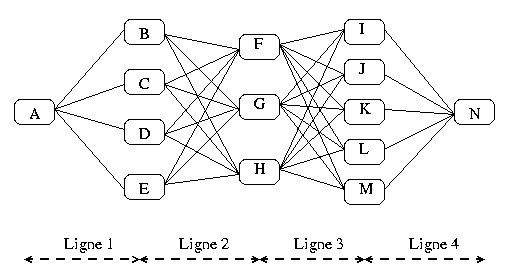
Sur ce graphe, chaque noeud représente un arrêt.
Les arrêts sur une colonne sont tous les points de contact entre les lignes de gauche et de droite (la ligne 1 et la ligne 2 sont en correspondance en B,C,D,A).
Les arcs représentent les voyages entre deux arrêts en utilisant la ligne écrite en dessous (Ex : de A à B en passant par la ligne 1).
Le but est de chercher le plus court chemin (en terme d'horaire) entre A et N et passant par L1..L4. Pour cela, sachant l'heure à laquelle on veut être en N, on en déduit l'heure à laquelle on doit être en I,J,K,L et M. Puis on propage, jusqu'à déterminer l'heure à laquelle on doit partir de l'arrêt de départ. Par la même occasion, on obtient les correspondances les plus efficaces.
Se reporter à : Formats