Les Octrees

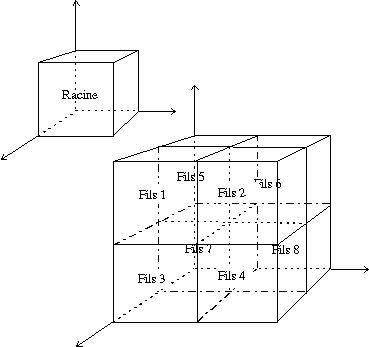
Pour cette méthode, l'espace des couleurs est représenté par un octree : arbre dont chaque noeud possède 8 fils.

Construction de l'arbre

• La racine de l'arbre représente l'ensemble des 256³ couleurs.
• Chaque fils est créé en découpant le cube en 8 parties égales :

On obtient un arbre de profondeur 8 dont chaque feuille représente un cube de coté 1 : une couleur unique. L'arbre complet contiendrait environ 20 millions de noeuds. Pour éviter cette démesure, on construit l'arbre au fur et à mesure du parcours de l'image, en créant pour chaque point de l'image la feuille qui le représente :

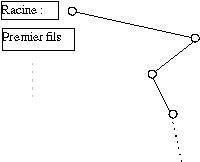Dans chaque noeud de l'arbre :

• On stocke la moyenne des couleurs que le noeud contient
• On note H, l'"énergie" du noeud : la somme des distances des couleurs contenues dans le noeud au centre du noeud.

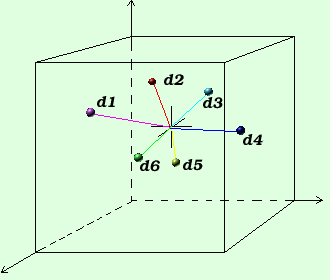
H = d1 + d2 + d3 + d4 + d5 + d6

Réduction de l'arbre : construction de E

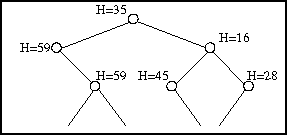
Le but de la quantification est de réduire le nombre de noeuds dans l'arbre : on cherche donc le noeud de plus petite énergie, c'est-à-dire celui dont le centre représente le mieux les couleurs internes.

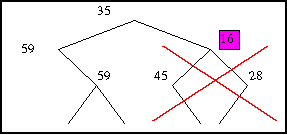
Et on supprime tous ses descendants.

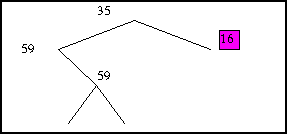
On répète le procédé jusqu'à ce qu'il y ait au plus 256 feuilles dans l'arbre.

En descendant dans l'arbre, on peut ainsi associer à chaque couleur de l'image originale une référence à la feuille qui la contient.

Construction de D

A chaque feuille de l'arbre réduit, on associe la moyenne des couleurs qu'elle représente.